CONSTRUCCIÓN DE POLÍGONOS REGULARES

1 DEFINICIÓN

En geometría, se denomina Polígono Regular, a una superficie cerrada, cuyos lados y ángulos interiores son congruentes entre sí. 

2. ELEMENTOS DE UN POLÍGONO REGULAR

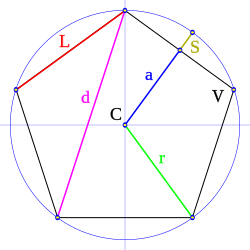
Lado: es cada uno de los segmentos que forman un polígono  (L)

Vértice: Punto de unión de dos lados consecutivos (C)

Radio: Segmento que une el centro del polígono con uno de sus vértices, si el polígono esta inscrito en una circunferencia y con la mediana, si el polígono esta circunscrito en la circunferencia. (r)

Apotema:Segmento perpendicular medido desde la mediana  hasta el centro de un polígono. (a)

Diagonal: Segmento que une dos vértices no continuos. (d)

Perímetro: Es la suma de los lados del polígono

Sagita: Linea comprendida entre el punto medio del lado del polígono 

Elementos de un polígono regular[editar]

• Lado, L: es cada uno de los segmentos que forman el polígono.
• Vértice, V: el punto de unión de dos lados consecutivos.
• Centro, C: el punto central equidistante de todos los vértices.
• Radio, r: el segmento que une el centro del polígono con uno de sus vértices.
• Apotema, a: segmento perpendicular a un lado, hasta el centro del polígono.
• Diagonal, d: segmento que une dos vértices no contiguos.
• Perímetro, P: es la suma de la medida de su contorno.
• Semiperímetro, SP: es la semisuma del perímetro.
• Sagita, S: parte del radio comprendida entre el punto medio del lado y el arco de circunferencia. La suma de la apotema: a más la sagita: S, es igual al radio: r.